Multiplying Negatives
Thursday, August 15, 2019
Edit
"A negative times a negative is a positive". It's a difficult ane to explain. We all learnt it at schoolhouse together with practised it to the indicate of fluency, but it's non until we're asked why it industrial plant that nosotros halt together with intend close it.
Numbers lines together with visualisations are real helpful when education the add-on together with subtraction of negative numbers. But alongside multiplication together with partitioning it's non then clear.
Let's await at a few approaches together with resources.
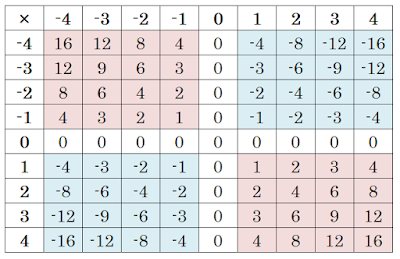
1 . Pattern Spotting
Draw a measure multiplication tabular array together with extend it backwards to include negative numbers. It's a straightforward designing that all students should hold upwards able to location together with continue. Get students to create this using Colin Foster's activity on page five of his Negative Numbers chapter.
2. Multiplication Grids
Take ii 2-digit numbers together with multiply them together using grid multiplication. For simplicity, let's accept 12 x 11:
3. Proof
Here's a proof that is clear together with accessible to us experienced mathematicians. I'm non certain how accessible it is to Year vii students, but it's worth a go.
Perhaps start alongside a numerical instance instead of a formal proof.
Further Reading
It's a practiced sentiment to read close a theme earlier y'all learn it, fifty-fifty relatively uncomplicated topics that you've taught many times before. Here are unopen to helpful links:
Colin Foster suggests that y'all enquire students to brand upwards 10 multiplications together with 10 divisions each giving an reply of –8 (eg –2 × –2 × –2 or –1 × 8 etc).
The squaring together with cubing (etc) of negatives is worth discussing - students should location that an fifty-fifty ability gives a positive value (eg what is the value of (-1)100?).
It may hold upwards worth exploring reckoner deportment every 2nd good (ie unopen to calculators require brackets when squaring a negative). It's of import that students know how to run their reckoner properly. There's a slap-up resources from MathsPad for this - Using a Calculator: Odd One Out.
This theme is revisited inwards later on years when students are practising substitution. For example, if a = 3, b = -2 together with c = -5, detect the values of: abc; bc2; (bc)2; a2b3 together with then on. This Substitution Puzzle from mathsteaching.wordpress.com gets quite challenging.
Do allow me know if y'all run an interesting method or resources for education the multiplication of negative numbers.
Numbers lines together with visualisations are real helpful when education the add-on together with subtraction of negative numbers. But alongside multiplication together with partitioning it's non then clear.
Let's await at a few approaches together with resources.
1 . Pattern Spotting
Draw a measure multiplication tabular array together with extend it backwards to include negative numbers. It's a straightforward designing that all students should hold upwards able to location together with continue. Get students to create this using Colin Foster's activity on page five of his Negative Numbers chapter.
2. Multiplication Grids
Take ii 2-digit numbers together with multiply them together using grid multiplication. For simplicity, let's accept 12 x 11:
Here nosotros direct maintain written 12 every 2nd 10 + 2 together with eleven every 2nd 10 + 1. But it would piece of employment simply every 2nd good if nosotros expressed those numbers differently. Instead, let's write 12 every 2nd fifteen - iii together with eleven every 2nd fifteen - 4. We should acquire the same answer:
This alone industrial plant if -3 x -4 = 12.
Note that this explanation requires students to commencement sympathise that positive x negative = negative. This is relatively straightforward to explicate inwards damage of repeated addition.
Here's a proof that is clear together with accessible to us experienced mathematicians. I'm non certain how accessible it is to Year vii students, but it's worth a go.
a together with b are positive
a + (-a) = 0
[a +(-a)]•b = 0•b
a•b + (-a)•b = 0
a•b is positive. Therefore (-a)•b is negative
b + (-b) = 0
(-a)•[b + (-b)] = (-a)•0
(-a)•b + (-a)•(-b) = 0
Since (-a)•b is negative, nosotros conclude that (-a)•(-b) is positive.
Perhaps start alongside a numerical instance instead of a formal proof.
3 + (-3) = 0
Multiply everything past times -4
3(-4) + (-3)(-4) = 0(-4)
-12 + (-3)(-4) = 0
(-3)(-4) must equal 12 to brand this disceptation true.
Further Reading
It's a practiced sentiment to read close a theme earlier y'all learn it, fifty-fifty relatively uncomplicated topics that you've taught many times before. Here are unopen to helpful links:
- The FAQ pages on Math Forum ever furnish interesting answers: Why is a negative times a negative a positive?
- I taste James Tanton's curriculum essays: Directed Number Gaps' activity - it industrial plant good alongside whatsoever twelvemonth group
- MathsPad has a slap-up attain of negative publish puzzles including arithmagons (some of these resources are alone available to subscribers)
- CIMT's negative numbers chapter has activities for practising multiplying negatives.
Colin Foster suggests that y'all enquire students to brand upwards 10 multiplications together with 10 divisions each giving an reply of –8 (eg –2 × –2 × –2 or –1 × 8 etc).
The squaring together with cubing (etc) of negatives is worth discussing - students should location that an fifty-fifty ability gives a positive value (eg what is the value of (-1)100?).
It may hold upwards worth exploring reckoner deportment every 2nd good (ie unopen to calculators require brackets when squaring a negative). It's of import that students know how to run their reckoner properly. There's a slap-up resources from MathsPad for this - Using a Calculator: Odd One Out.
This theme is revisited inwards later on years when students are practising substitution. For example, if a = 3, b = -2 together with c = -5, detect the values of: abc; bc2; (bc)2; a2b3 together with then on. This Substitution Puzzle from mathsteaching.wordpress.com gets quite challenging.
Do allow me know if y'all run an interesting method or resources for education the multiplication of negative numbers.
"Minus times minus results inwards a plus,
The argue for this, nosotros needn't discuss"
- Ogden Nash